Vaibhavi Mutya

Graduate Studies Blog

6 minute read

Regression and Simpsons Paradox

Overview

In this project, I breifly explain regression from function approximation and probabilitic viewpoints and then model SalesPrice from the Ames housing dataset using simple linear regression, implemented from scratch in python for both categorical/continous features. Thereafter, I plot the feature estimators from best to worst and explain simpson’s paradox observed during the process.

Data

Dataset used is an AmesHousing.txt of category population which consists of 2930 rows and 82 features among them 23 nominal, 23 ordinal, 14 discrete, and 20 continuous variables (and 2 additional observation identifiers). The dataset used is of the year 2006 - 2010.

Linear Regression Overview

Function Approximation Viewpoint

From a function approximation viewpoint, regression can be defined as learning a function \({y}=f(X)\) where y is the response and X are the set of features.

The form of this function is linear in nature,

\[{y} = \beta_0 + \beta_1 x_1, \beta_2 x_2, ... \beta_k x_k + \epsilon\]

\(\beta_0\) is the bias term
\(\beta's\) are the weights
\(\epsilon\) is the error (b/w our linear predictor and true response), and we make some assumption on the error term namely:

  1. Zero mean and constant Var i.e \(\approx N(0, \sigma^2)\) \
  2. Independent across observations.

Regularization is the process where we apply constraints (usually p-norm’s) on the model parameters (\(\beta's\)). Depending on the norm used (L1,L2) we call them lasso or ridge regression respectively.

Probabilistic Viewpoint

From a probabilitic viewpoint, we can rewrite the model as a conditional probability density:

\[p(y | X, \theta) = N(y| \mu(X), \sigma^2(X))\]

For linear regression, we model \(y\) using a normal distribution. Further, we assume mean (\(\mu\)) is a linear function of \(X\), so \(\mu = \beta^TX\) and that the variance is constant.

We can extend this framework, by modeling \(y\) using another distribution from the exponential family (eg: poisson, bernoulli etc.) and that is known as Generalized Linear Models.

Problem we are trying to solve:

Here, we model the dependence of y (SalesPrice) on each of the features in our data set using a normal distribution (linear regression).

Regression with categorical features

We will model the dependence of \(y\) on \(x\) as a normal distribution whose mean (but not variance) depends on the value of \(x\), with one separate mean parameter for each category of \(x\).

\[p(y\mid x) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{1}{2\sigma^2}(y-\mu_x)^2}\]

Maximum likelihood estimate for \(\mu_1, \mu_2, \dots, \mu_K\) and \(\sigma^2\) is

\[\hat{\mu}_j= \frac{\sum_{i | x_i = j} y_i}{\sum_{i | x_i = j} 1}\] \[\hat{\sigma}^2 = \frac{1}{m}\sum_{i=1}^m (y_i - \hat{\mu}_{x_i})^2\]

That is, the maximum likelihood estimate for \(\mu_j\) is the average of all of the \(y\) values when \(x=j\), and the maximum likelihood estimate for the variance is the empirical average squared difference between these means (predictions) and the true values.

Implementing the above from scratch and ordering from lowest variance to highest i.e from best single-feature estimator to worst.

# MLE function for categorical variables
def categorical_mle(input_feature, response):
  v = np.unique(input_feature)

  #Get mu_j for all j of a feature
  category_means = []
  for i in v:
    response_by_category = []
    for j,k in zip(input_feature, np.arange(len(response))):
      if j == i:
        response_by_category.append(response[k])
    category_means.append(np.average(response_by_category))

  #Get variance for the feature
  variance_for_each = []
  for a,b in zip(v, np.arange(len(v))):
    for c,d in zip(input_feature, np.arange(len(response))):
      if c == a:
        variance_for_each.append(np.square(response[d] - category_means[b]))
  overall_variance = np.average(variance_for_each)

  return(category_means, overall_variance)

# ordering output from lowest to highest variance (best single-feature estimator)

mu_sigma_list = []
for i in range(X[:, iscat].shape[1]):
  mu_sigma_list.append(categorical_mle(X[:, iscat][:, i], X[:, -1]))


sigma_list = [i[1] for i in mu_sigma_list]
mu_list = [i[0] for i in mu_sigma_list]

keys_sigma = [str(i) for i in range(X[:, iscat].shape[1])]
values_sigma = sigma_list
values_mu = mu_list
dictionary_sigma = dict(zip(keys_sigma, values_sigma))
dictionary_mu = dict(zip(keys_sigma, values_mu))

dictionary_sigma_asc = sorted(dictionary_sigma, key=dictionary_sigma.get)
dictionary_sigma_asc_int = [int(i) for i in dictionary_sigma_asc]

fig, axs = plt.subplots(7,7, figsize=(35, 10), facecolor='w', edgecolor='k')
fig.subplots_adjust(hspace = .5, wspace=.001)
fig.tight_layout(rect=[0, 0.03, 1, 0.95])

axs = axs.ravel()

for i,j,k in zip(np.arange(X[:, iscat].shape[1]), dictionary_sigma_asc_int, dictionary_sigma_asc):
    axs[i].scatter(X[:, iscat][:, j], X[:, -1], color = 'black')
    axs[i].scatter(np.unique(X[:, iscat][:, j]), dictionary_mu[k], color = 'blue')
    axs[i].set_title(dictionary_sigma[k])
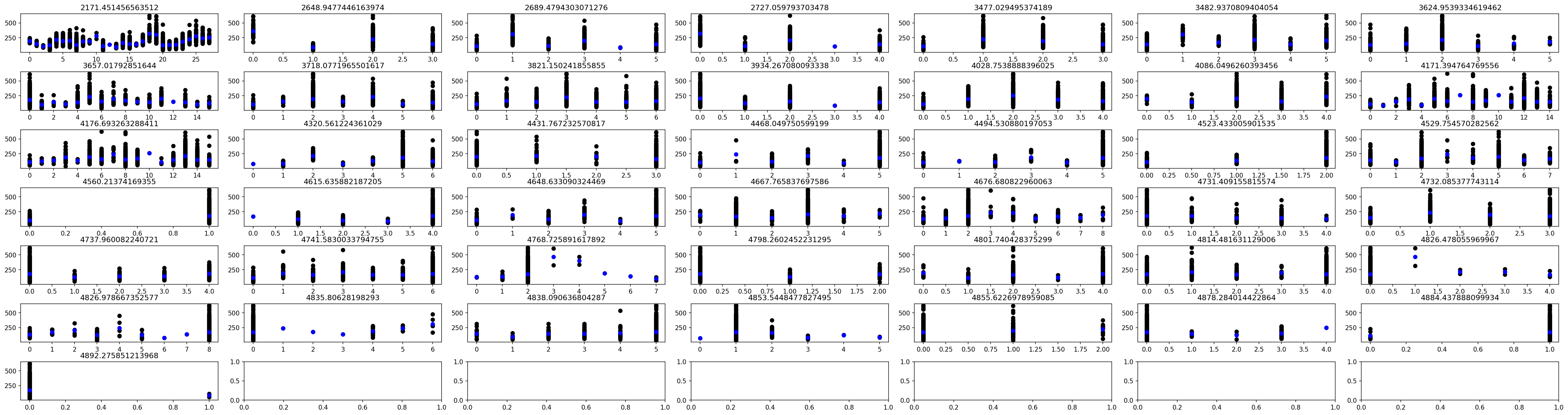
my alt text

Regression with continuous features

Same thing as above but for continuous features.

\[p(y\mid x) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{1}{2\sigma^2}(y - (ax+b))^2}\]

This is regular regression.

Implementing the above from scratch and ordering from lowest variance to highest i.e from best single-feature estimator to worst.


#Simple linear regression using closed form solution
def beta_o(b_1, y, x):
  beta_o = np.average(y) - b_1 * np.average(x)
  return(beta_o)

def beta_1(y , x):
  y_bar = np.average(y)
  x_bar = np.average(x)

  num = np.sum((y - y_bar) * (x - x_bar))
  denom = np.sum(np.square((x - x_bar)))

  beta_1 = num / denom

  return(beta_1)

def model(b0, b1, x_new):
  Y = b0 + (b1 * x_new)
  return(Y)

# Ordering from lowest to higest variance (best single-feature estimator)

not_cat = np.logical_not(iscat)

keys_cont = [str(i) for i in range(X[:, not_cat].shape[1])]
values_b0 = []
values_b1 = []
variance_estimate_list = []
y_hat_list = []

for i in range(X[:, not_cat].shape[1]):
  #remove nulls
  mask = np.logical_not(np.isnan(X[:, not_cat][:, i]))
  non_null_X = X[:, not_cat][:, i][mask]
  b1 = beta_1(X[:, -1][mask] , non_null_X)
  b0 = beta_o(b1, X[:, -1][mask], non_null_X)
  values_b0.append(b0)
  values_b1.append(b1)

  y_hat = [model(b0, b1, j) for j in non_null_X]
  y_hat_list.append(y_hat)
  variance_estimate = np.average(np.square(X[:, -1][mask] - y_hat))
  variance_estimate_list.append(variance_estimate)


dictionary_b0 = dict(zip(keys_cont, values_b0))
dictionary_b1 = dict(zip(keys_cont, values_b1))
dictionary_variance_estimate = dict(zip(keys_cont, variance_estimate_list))
dictionary_yhat =  dict(zip(keys_cont, y_hat_list))


dictionary_variance_asc = sorted(dictionary_variance_estimate, key=dictionary_variance_estimate.get)
dictionary_variance_asc_int = [int(i) for i in dictionary_variance_asc]

fig, axs = plt.subplots(8,5, figsize=(35, 10), facecolor='w', edgecolor='k')
fig.subplots_adjust(hspace = .5, wspace=.001)
fig.tight_layout(rect=[0, 0.03, 1, 0.95])

axs = axs.ravel()

for i,j,k in zip(np.arange(X[:, not_cat].shape[1]), dictionary_variance_asc_int, dictionary_variance_asc):
    axs[i].scatter(X[:, not_cat][:, j], X[:, -1], color = 'black')
    plotline(axs[i], dictionary_b1[k], dictionary_b0[k])
    axs[i].set_title(dictionary_variance_estimate[k])
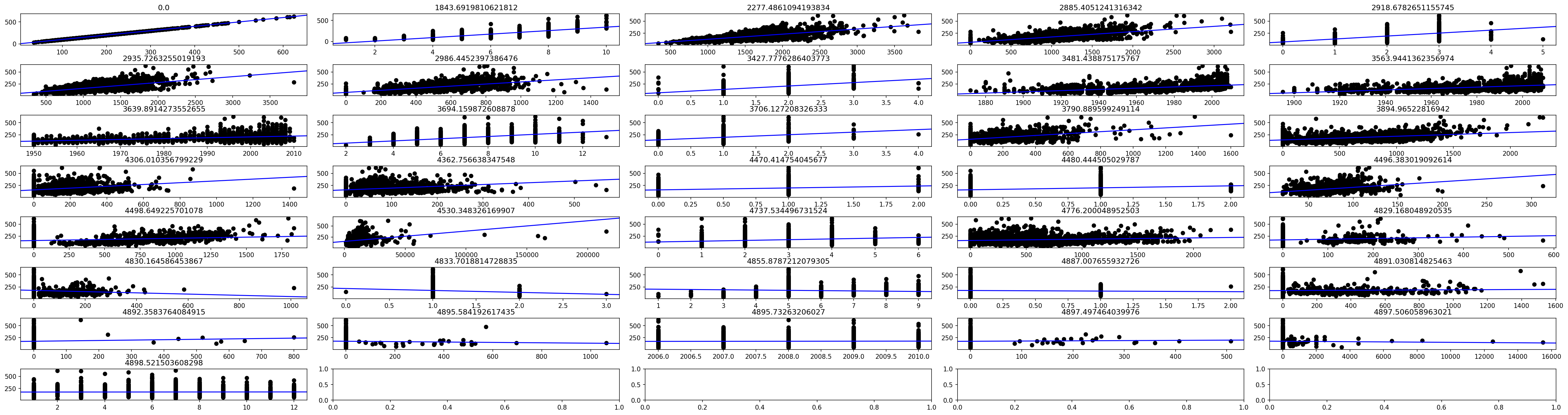
my alt text

Some nuances:

  • Some continuous-valued features had missing values which are encoded as ‘Nan’. I omit those examples (from both 𝑦 and 𝑥) when calculating the regression coefficients for that feature. The numpy function I used to do so is np.isnan(v) which returned a boolean-valued vector that is True where value is NaN and False otherwise.
  • Some continuous-valued features did not have any variation. That is, 𝑥 is a constant. This makes it impossible to estimate a slope. Therefor I set 𝑎=0 and 𝑏 to be the mean of the feature.
  • If there are no points at all left after removing NaNs, then there isn’t really a regression problem. In this case I just let 𝑎=0 and 𝑏=0.

Simpsons Paradox

We observe a very interesting phenomena here, there is a negative correlation between the number of kitchens (feature “Kitchen AbvGr”) and the selling price. Does this mean that if I add a kitchen to my home, it will cause it to sell for less money? Or, that if I have two kitchens removing one before selling will increase the price?

No, the above reasoning is incorrect. In the above statement we are interpreting the effect of Kitchen AbvGr on Selling price causally. Hence the incorrect statement.

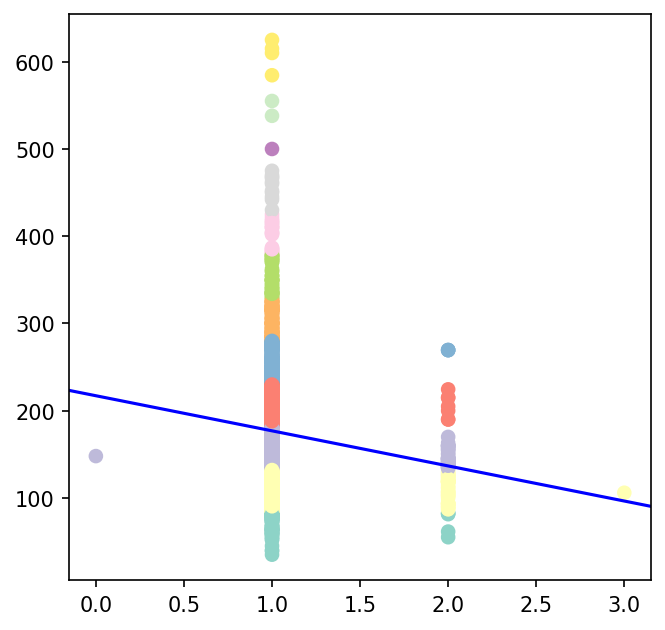
my alt text
This paradox can be resolved by conditioning on appropriate event spaces. When we look at P(SalesPrice Kitchen AbvGr), at a holistic level the correlation between Kitchen AbvGr and Sales Price is negative (-40 is the slope) but when we condition on Neighbourhood we see that, Houses with 2 kitchens are from specific neighbourhoods which have low cost in general therefore for these neighbourhoods (see color carefully) the sales price is low. Compared to light green, yellow and purple for which cost is hight. Therefore, if we condition on P(SalesPrice Kitchen AbvGr, Neighbourhood = light green, yellow and purple) we will get a positive correlation.

Updated:

You may also enjoy

Linear classifier from scratch

5 minute read

Introduction In this project I build a linear classifier from scratch using MNIST dataset (a standard digit classification dataset). Given a 28 \(\times\) 28...